Ecuación Diferencial Exacta

 Ecuaciones Diferenciales Exactas

Definición:

En matemáticas, una ecuación diferencial exacta es una ecuación diferencial ordinaria de primer orden que presenta la forma:

 M (x,y)dx + N(x,y)dy=o

donde las derivadas parciales de las funciones M y N: y son iguales. Esto es equivalente a decir que existe una función 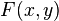tal que:

donde y .


Dado que 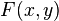es una función diferenciable, entonces, por el teorema de Clairaut, sus derivadas cruzadas deben ser iguales. Esto significa que:
.

Algoritmo:

Primero definimos si la ecuacion es exacta o no, mediante los siguiente dos
criterios:

• FORMA ESTÁNDAR DE LA ED EXACTA

M(x,y)dx+N(x,y)dy=0

• CRITERIO PARA DEFINIR EXACTITUD DE LA ED

δMδy=δNδx
       Paso 1: Integrar a la función M son respecto a "x"  y sustituir a la constante C por la funcion    c=h(y)

F(x,y)=∫M(x,y)dx+g(y)

Paso 2:  Se deriva a la funcion encotrada con respecto a "y" y se iguala con la  función

 δδy∫M(x,y)dx+g′(y)=N(x,y)

Paso 3:   Se integra la función con respecto a la variable "y" y se despeja

 g(y)=∫N(x,y)dy−∫δδy∫M(x,y)dxdy

Paso 4: Se encuentra la solución general con la ecuación del paso 1 sustituyendo el valor de "h" de "y" e igualamos con una constante de integración

 Sustituimos g(y) del paso (3) en (1) e igualamos a c (c = constante)

 ∫M(x,y)dx+g(y)=c




Eejmplo: 

(5x+4y)dx+(4x−8y)dy=0

-Determinamos si es exacta la ED

 M(x,y)dx=5x+4y;        N(x,y)=4x−8y

δMδy=4;        δNδx=4

-De donde concluimos que la ecuación si es exacta ya que:

Resolvemos la ecuación de acuerdo a los pasos listados anteriorment

δMδy=δNδx

e


Paso 1.

∫M(x,y)dx+g(y)===∫(5x+4y)dx+g(y)5∫xdx+4y∫dx+g(y)52x2+4xy+g(y)

Paso 2.

δδy∫M(x,y)dx+g′(y)⇒δδy(52x2+4xy)+g′(y)⇒0+4x+g′(y)⇒0+g′(y)g′(y)=====N(x,y)4x−8y34x−8y3−8y3−8y3

Paso 3.

g(y)g(y)====∫N(x,y)dy−∫δδy∫M(x,y)dxdy−8∫y3dy–84y4−2y4

Paso 4.

∫M(x,y)dx+g(y)52x2+4xy−2y4==cc

La solución es:
52x2+4xy−2y4=c


Solución particular: Si fijando cualquier punto P(X0,Y0) por donde debe pasar necesariamente la solución de la ecuación diferencial, existe un único valor de C, y por lo tanto de la curva integral que satisface la ecuación, éste recibirá el nombre de solución particular de la ecuación en el punto P(X0,Y0), que recibe el nombre de condición inicial. Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.